Tetrakis hexahedron
| Tetrakis hexahedron | |
|---|---|
(Click here for rotating model) |
|
| Type | Catalan solid |
| Face type | isosceles triangle |
| Faces | 24 |
| Edges | 36 |
| Vertices | 14 |
| Vertices by type | 6{4}+8{6} |
| Face configuration | V4.6.6 |
| Symmetry group | Oh, [4,3], *432 |
| Dihedral angle | 143°7'48"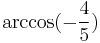 |
| Properties | convex, face-transitive |
Truncated octahedron (dual polyhedron) |
Net |
In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube.
It also can be called a disdyakis hexahedron as the dual of an omnitruncated tetrahedron.
Contents |
Uses
Naturally occurring (crystal) formations of tetrahexahedrons are observed in copper and fluorite systems.
Polyhedral dice shaped like the tetrakis hexahedron are occasionally used by gamers.
A 24-cell viewed under a vertex-first perspective projection has a surface topology of a tetrakis hexahedron and the geometric proportions of the rhombic dodecahedron, with the rhombic faces divided into two triangles.
Gallery
See also
- Disdyakis triacontahedron
- Disdyakis dodecahedron
- Bisected hexagonal tiling
- Compound of three octahedra
References
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR730208 (The thirteen semiregular convex polyhedra and their duals, Page 14, Tetrakishexahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Tetrakis hexahedron )
External links
- Eric W. Weisstein, Tetrakis hexahedron (Catalan solid) at MathWorld.
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- VRML model
- Conway Notation for Polyhedra Try: "dtO"
- Tetrakis Hexahedron -- Interactive Polyhedron model
- The Uniform Polyhedra
|
||||||||||||||||||||||||||